Show code cell source
import pathlib
import pandas as pd
import numpy as np
import jupedsim as jps
from shapely import Polygon
import shapely
import pedpy
import matplotlib.pyplot as plt
# from matplotlib.patches import Circle
from typing import List, Tuple, Dict
%matplotlib inline
Simulating Single-File Movement#
Pedestrian dynamics often focuses on the relationship between two key variables: density and either flow or velocity. The relationship is often visualized in what’s termed as the fundamental diagram. By quantifying the capacity of pedestrian facilities, it serves as an essential tool for evaluating escape routes in emergencies and determining the effectiveness of various pedestrian movement models when depicting pedestrian streams.
A fundamental question arises: how does one investigate the intricacies of the fundamental diagram without the interference of external factors?
Single-file movement presents the simplest possible system in pedestrian dynamics. It is envisioned as the unidirectional motion of individuals moving along a straight line, thereby considerably reducing the degrees of freedom. In essence, by stripping down the system to this basic representation, it limits the external factors that might affect the outcomes. As a result, any observations or patterns detected can be attributed with higher confidence to the direct interplay between density and flow, providing a clearer understanding of the fundamental diagram.
In this tutorial, we’ll simulate with JuPedSim a simplified geometry with closed boundary conditions acording to Paetzke.
Show code cell source
def generate_oval_shape_points(
num_points: int,
length: float = 2.3,
radius: float = 1.65,
start: Tuple[float, float] = (0.0, 0.0),
dx: float = 0.2,
threshold: float = 0.5,
):
"""Generate points on a closed setup with two segments and two half circles."""
points = [start]
selected_points = [start]
last_selected = start # keep track of the last selected point
# Define the points' generating functions
def dist(p1, p2):
return ((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2) ** 0.5
# Calculate dphi based on the dx and radius
dphi = dx / radius
center2 = (start[0] + length, start[1] + radius)
center1 = (start[0], start[1] + radius)
npoint_on_segment = int(length / dx)
# first segment
for i in range(1, npoint_on_segment + 1):
tmp_point = (start[0] + i * dx, start[1])
points.append(tmp_point)
if dist(tmp_point, last_selected) >= threshold:
selected_points.append(tmp_point)
last_selected = tmp_point
# first half circle
for phi in np.arange(-np.pi / 2, np.pi / 2, dphi):
x = center2[0] + radius * np.cos(phi)
y = center2[1] + radius * np.sin(phi)
tmp_point = (x, y)
points.append(tmp_point)
if dist(tmp_point, last_selected) >= threshold:
selected_points.append(tmp_point)
last_selected = tmp_point
# second segment
for i in range(1, npoint_on_segment + 1):
tmp_point = (
start[0] + (npoint_on_segment + 1) * dx - i * dx,
start[1] + 2 * radius,
)
points.append(tmp_point)
if dist(tmp_point, last_selected) >= threshold:
selected_points.append(tmp_point)
last_selected = tmp_point
# second half circle
for phi in np.arange(np.pi / 2, 3 * np.pi / 2 - dphi, dphi):
x = center1[0] + radius * np.cos(phi)
y = center1[1] + radius * np.sin(phi)
tmp_point = (x, y)
points.append(tmp_point)
if dist(tmp_point, last_selected) >= threshold:
selected_points.append(tmp_point)
last_selected = tmp_point
if dist(selected_points[-1], start) < threshold:
selected_points.pop()
if num_points > len(selected_points):
print(f"warning: {num_points} > Allowed: {len(selected_points)}")
selected_points = selected_points[:num_points]
return points, selected_points
_, exterior = generate_oval_shape_points(
48, radius=1.65 + 0.4, start=(0, -0.4), threshold=0.2
)
_, interior = generate_oval_shape_points(
35, radius=1.65 - 0.4, start=(0, 0.4), threshold=0.2
)
walkable_area = pedpy.WalkableArea(
shapely.difference(Polygon(exterior), Polygon(interior))
)
def find_nearest_clockwise_waypoint(position, all_points, waypoints):
idx = all_points.index(position)
while True:
idx = (idx + 1) % len(all_points)
if all_points[idx] in waypoints:
return all_points[idx]
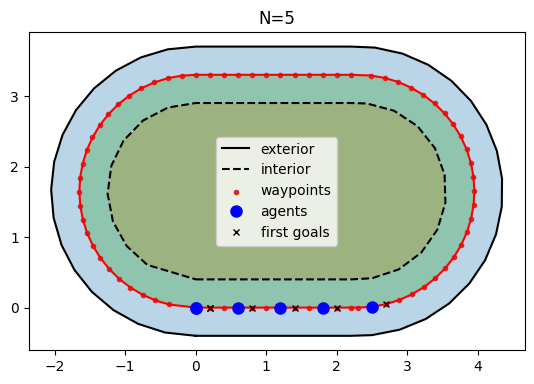
Scenario Overview#
Let’s begin by positioning \(N\) agents along the central path within our specified geometry. This particular geometry presents an interesting challenge; though our goal is to simulate a movement akin to 1D, where agents traverse a straight line, the line here is bent.
We will set up the waypoints and agent positions based on the circuit illustrated by the dashed line in the preceding figure.
Each agent will be assigned its initial waypoint to aim for.
def distribute_agents_and_waypoints(total_agents: int):
all_waypoints, positions = generate_oval_shape_points(
num_points=total_agents
)
first_waypoints = []
for position in positions:
first_waypoints.append(
find_nearest_clockwise_waypoint(
position, all_waypoints, all_waypoints
)
)
return all_waypoints, first_waypoints, positions
Show code cell source
def plot_points_and_polygons(
all_waypoints, choosen_waypoints, exterior, interior, positions
):
__file__, ax = plt.subplots(ncols=1, nrows=1)
ax.set_aspect("equal")
x_exterior, y_exterior = Polygon(exterior).exterior.xy
plt.plot(x_exterior, y_exterior, "-k", label="exterior")
plt.fill(x_exterior, y_exterior, alpha=0.3)
x_interior, y_interior = Polygon(interior).exterior.xy
plt.plot(x_interior, y_interior, "--k", label="interior")
plt.fill(x_interior, y_interior, alpha=0.3)
x_awp, y_awp = Polygon(all_waypoints).exterior.xy
plt.plot(x_awp, y_awp, "-r")
plt.fill(x_awp, y_awp, alpha=0.3)
plt.scatter(*zip(*all_waypoints), marker=".", label="waypoints")
x_agents, y_agents = Polygon(positions).exterior.xy
plt.plot(x_agents, y_agents, "ob", ms=8, label="agents")
x_wp, y_wp = Polygon(choosen_waypoints).exterior.xy
plt.plot(x_wp, y_wp, "xk", ms=5, label="first goals")
plt.legend()
plt.title(f"N={len(positions)}")
plt.show()
Show code cell source
def compute_unit_vector(new_pos, wp):
dx = wp[0] - new_pos[0]
dy = wp[1] - new_pos[1]
magnitude = (dx**2 + dy**2) ** 0.5
if magnitude == 0:
return (0, 0)
ux = dx / magnitude
uy = dy / magnitude
return (ux, uy)
Defining the Journey#
For our simulation, we’re aiming for movement within a closed system. To achieve this, we’ll establish a cyclical transition between waypoints, allowing agents to seamlessly move from one waypoint to the next. Given this structure, agents are confined within the system, eliminating the need for exit points.
While the starting orientation of our agents might not play a pivotal role, we’ll still configure it for precision. This means that, from the outset, each agent will be oriented towards its initially selected waypoint.
def init_waypoints(
simulation, all_waypoints: List[Tuple[float, float]]
) -> Dict[Tuple[float, float], id]:
waypoint_ids = []
waypoints: Dict[Tuple[float, float], id] = {}
distance = 0.1
for waypoint in all_waypoints:
wp_id = simulation.add_waypoint_stage(waypoint, distance)
waypoint_ids.append(wp_id)
waypoints[waypoint] = wp_id
return waypoints
def init_journey(
simulation: jps.Simulation, waypoints: Dict[Tuple[float, float], id]
) -> int:
waypoint_ids = list(waypoints.values())
journey = jps.JourneyDescription(waypoint_ids)
# create a circular transition from wp to next wp
for idx, waypoint in enumerate(waypoint_ids):
next_waypoint = (
waypoint_ids[0]
if idx == len(waypoint_ids) - 1
else waypoint_ids[idx + 1]
)
journey.set_transition_for_stage(
waypoint, jps.Transition.create_fixed_transition(next_waypoint)
)
journey_id = simulation.add_journey(journey)
return journey_id
def add_model_to_simulation(
simulation: jps.Simulation,
positions,
choosen_waypoints,
waypoints: Dict[Tuple[float, float], id],
journey_id: int,
) -> None:
agent_parameters = jps.CollisionFreeSpeedModelAgentParameters()
agent_parameters.journey_id = journey_id
for wp, new_pos in zip(choosen_waypoints, positions):
agent_parameters.position = new_pos
agent_parameters.stage_id = waypoints[wp]
simulation.add_agent(agent_parameters)
Executing the Simulation#
Now, we’ll proceed to run our simulation up to a predefined maximum iteration count. This approach lets the internal dynamics stabilize, potentially reaching a steady state. However, it’s worth noting that certain dynamics, like stop-and-go waves, might prevent the system from settling into such a state.
def run_simulation(total_agents: int, number_iterations: int = 2000):
(
all_waypoints,
first_waypoints,
positions,
) = distribute_agents_and_waypoints(total_agents)
plot_points_and_polygons(
all_waypoints, first_waypoints, exterior, interior, positions
)
trajectory_file = f"single-file-{total_agents}.sqlite"
simulation = jps.Simulation(
dt=0.05,
model=jps.CollisionFreeSpeedModel(
strength_neighbor_repulsion=2.6,
range_neighbor_repulsion=0.1,
range_geometry_repulsion=0.05,
),
geometry=exterior,
excluded_areas=interior,
trajectory_writer=jps.SqliteTrajectoryWriter(
output_file=pathlib.Path(trajectory_file),
),
)
waypoints = init_waypoints(simulation, all_waypoints)
journey_id = init_journey(simulation, waypoints)
add_model_to_simulation(
simulation, positions, first_waypoints, waypoints, journey_id
)
while simulation.iteration_count() < number_iterations:
simulation.iterate()
return trajectory_file
trajectory_files = [run_simulation(N) for N in [5, 15, 20, 24]]
from jupedsim.internal.notebook_utils import animate, read_sqlite_file
for trajectory_file in trajectory_files:
trajectories, walkable_area_sqlite = read_sqlite_file(trajectory_file)
animate(trajectories, walkable_area, every_nth_frame=5).show()